You're reading the documentation for a development version. For the latest stable documentation, please have a look at v5.1.X. For the latest pre-release documentation, please have a look at v6.0.0-alpha.1.
Fragmentation Models¶
For detailed information on the crystallization models implemented in CADET, including aggregation, please refer to [30].
The fragmentation/breakage model considered here can be combined with Primary Particle Formation and/or Aggregation Models. Further, it can be applied in any of the unit operations, specifically in a STR or DPFR.
The fragmentation/breakage is governed by the fragmentation equation and describes the evolution of the particle number density \(n\) changes due to fragmentation/breakage. Here, we consider multiple fragmentation, i.e. the general breakage of a particle into a particle size distribution, based on particle size \(x\), which is called internal coordinate.
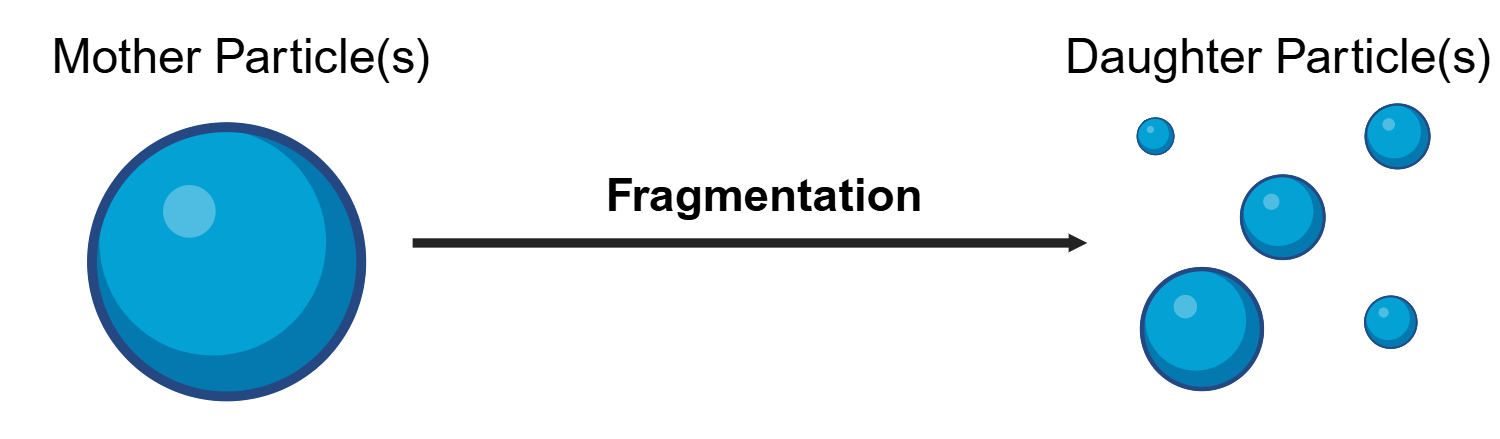
Fig. 10 Particle fragmentation/breakage considered in the fragmentation equation.¶
Size-based fragmentation is governed by
Here, \(x_{\mathrm{end}}\) is the maximal considered particle size, \(b(x | \lambda)\) is the probability density function for the generation of a particle of size \(x\) from breakage of a particle of size \(\lambda\), and \(S\) is the selection function which determines the rate of fragmentation.
where \(\alpha > 0\) reckons the breakage rate as a function of particle volume.
The propability breakage function is defined as
where \(\gamma > 1\) determines the average number of daughter particles into which a mother particle breaks. Further, \(b\) satisfies
where \(N(\lambda)\) is the total number of daughter particles that a mother particle of size \(\lambda\) generates on average.
For information on model parameters and how to specify the model interface, see Crystallization / Precipitation models.