You're reading the documentation for a development version. For the latest stable documentation, please have a look at v5.1.X. For the latest pre-release documentation, please have a look at v6.0.0-alpha.1.
Aggregation Models¶
For detailed information on the crystallization models implemented in CADET, including aggregation, please refer to [30].
The aggregation model can be combined with Primary Particle Formation and/or Fragmentation Models. Further, it can be applied in any of the unit operations, specifically in a STR or DPFR.
The aggregation is governed by the Smoluchowski coagulation equation and describes the evolution of the particle number density \(n\) changes due to agglomeration/aggregation. Here, we consider binary particle aggregation based on particle size \(x\), which is called internal coordinate.
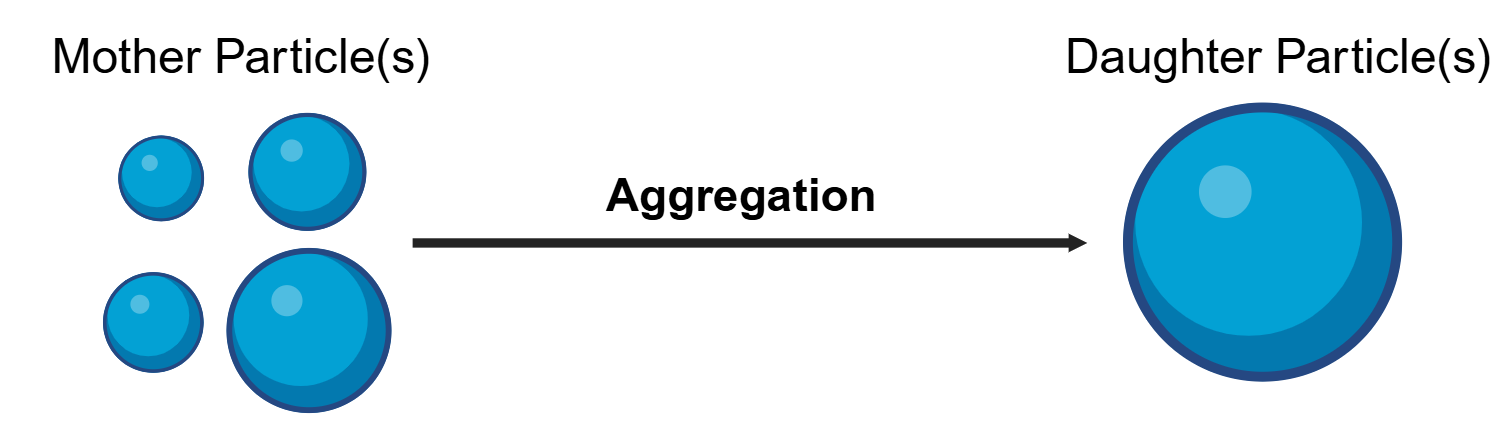
Fig. 9 Particle agglomeration/aggregation considered in the Smoluchowski coagulation equation.¶
The size-based aggregation equation roots in the classical volume based Smoluchowski coagulation equation, which we transform to a size-based equation using the identity
which identifies the change of particle count within a volume interval \([k_vx^3, k_vx^3+d(k_vx^3)]\) with the change of particle count within a size interval \([x,x+dx]\).
Size-based binary aggregation is governed by the Smoluchowski coagulation equation
Here, \([x_{c}, x_{\mathrm{end}}]\) is the considered particle size interval, \(\beta(x,\lambda)\) is the aggregation kernel specific to the underlying aggregation mechanism of your system.
Five kernels are already implemented in CADET. They include:
- Constant kernel
- \[\beta(x, \lambda) = \beta_0\]
- Brownian kernel
- \[\beta(x, \lambda) = \beta_0 \frac{(x + \lambda)^2}{x \lambda}\]
- Smoluchowski kernel
- \[\beta(x, \lambda) = \beta_0 (x + \lambda)^3\]
- Golovin kernel
- \[\beta(x, \lambda) = \beta_0 (x^3 + \lambda^3)\]
- Differential force kernel
- \[\beta(x, \lambda) = \beta_0 (x + \lambda)^2 (x^2 - \lambda^2)\]
where \(\beta_0 > 0\) is the aggregation rate constant. Please reach out to us for customized aggregation kernels.
For information on model parameters and how to specify the model interface, see Crystallization / Precipitation models.