Population Balance Models

The population balance model (PBM) is given by a particle-number continuity equation which describes the evolution of the number density \(n\) of the particles over time \(t\) and with respect to a so-called internal coordinate \(x\) and external coordinate \(z\). The internal coordinate can be chosen as any characteristic property of the particles such as the particle size or volume. The external coordinate can be a characteristic dimension of the reactor itself, including its axial length.

In CADET, we chose particle size and axial coordinate as the internal and external coodinate respectively. The PBM in CADET is implemented so that it can be used in any unit operation that supports reactions. Typical applications consider crystallization in a CSTR or, to model continuous processes, in a Dispersive Plug-Flow Reactor (DPFR), which is described by the LRM without solid phase.

In the following, we give a brief overview on the modelling equations, for more information on the PBM as implemented in CADET, please refer to [24].

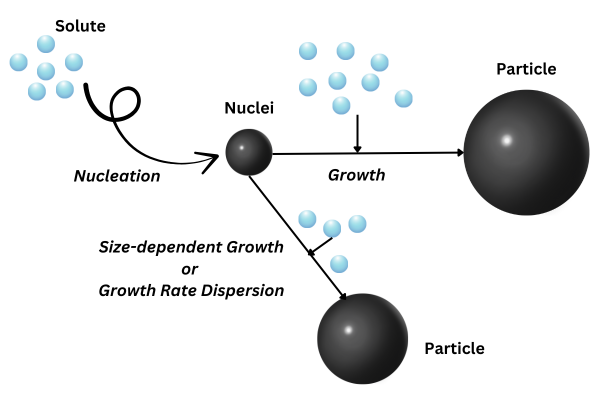
Fig. 8 Nucleation, growth and growth rate dispersion in PBM. Note that dispersion is used to model (random) variance in growth speed, not the reduction of particle size, which is feasible for a convection dominated process.

Population Balance Model in a CSTR

We assume a well-mixed tank and choose the particle size \(x\in (x_c, \infty)\) as the internal coodinate, with \(x_c>0\) being the minimal particle size considered. The corresponding PBM is given as

\[\begin{aligned} \frac{\partial (n V)}{\partial t} = F_{in}n_{in} - F_{out}n - V \left( \frac{\partial (v_{G}n)}{\partial x} - D_g \frac{\partial^2 n}{\partial x^2} - B_0 \delta (x-x_c) \right), \end{aligned}\]

where \(F_{in}, F_{out}\in \mathbb{R}^+\) are the volumetric inflow and outflow rates, \(V\in\mathbb{R}^+\) is the reactor volume, \(n(t, x)\colon [0, T_\text{end}] \times (x_c, \infty) \mapsto \mathbb{R}^+\) is the number density distribution, \(n_{in}\in\mathbb{R}^+\) is the number density distribution of the inlet feed, \(v_{G}\in\mathbb{R}^+\) is the particle growth rate, \(D_g\in\mathbb{R}^+\) is the growth dispersion rate.

The boundary conditions are given by the regularity boundary condition

(27)\[\begin{aligned} \left. \left( nv_{G} - D_g \frac{\partial n}{\partial x} \right) \right|_{x \to \infty}=0, \end{aligned}\]

and the nucleation kinetics boundary condition

(28)\[\begin{aligned} \left. \left( nv_{G}-D_g \frac{\partial n}{\partial x} \right)\right|_{x=x_c} = B_0, \end{aligned}\]

where \(B_0\in\mathbb{R}^+\) is the nucleation kinetics factor representing particle nucleations of size \(x_c\in\mathbb{R}^+\).

The model is complemented by the following mass balance equation which accounts for the mass transfer between the particle phase and the solute phase

\[\begin{aligned} \frac{\partial (cV)}{\partial t} = F_{in}c_{in} - F_{out}c -\rho k_v V \left( B_0x^3_c + 3\int_{x_c}^{\infty} v_{G}n\ x^2 \;\mathrm{d}x \right), \end{aligned}\]

where \(c(t)\colon [0, T_\text{end}] \mapsto \mathbb{R}^+\) is the solute concentration in the bulk phase, \(c_{in}\in\mathbb{R}^+\) is the inlet solute mass concentration, \(\rho > 0\) is the nuclei mass density and \(k_v > 0\) is the volumetric shape factor of the particles.

Evolution of the reactor’s volume is governed by

\[\begin{aligned} \frac{\mathrm{d}V}{\mathrm{d}t} &= F_{\text{in}} - F_{\text{out}}. \end{aligned}\]

Population Balance Model in a DPFR

The PBM can also be formulated for a DPFR to model continuous processes. That is, we choose the axial position within a DPFR as the external coordinate \(z\in[0, L]\) and formulate the \(2D\) PBM

\[\begin{aligned} \frac{\partial n}{\partial t} = -v_\text{ax} \frac{\partial n}{\partial z} +D_{ax} \frac{\partial^2 n}{\partial z^2} - \frac{\partial (v_{G}n)}{\partial x} + D_g \frac{\partial^2 n}{\partial x^2}, \end{aligned}\]

where \(n(t, x, z)\colon [0, T_\text{end}] \times (x_c, \infty) \times [0, L] \mapsto \mathbb{R}^+\) is the number density distribution, \(v_\text{ax}\in\mathbb{R}^+\) is the axial velocity and \(D_{ax}\in\mathbb{R}^+\) is the axial dispersion coefficient.

Boundary conditions for the internal coordinate are again given by Eq. 27 and Eq. 28.

For the external coordinate \(z\), Danckwerts boundary conditions are applied:

\[\begin{aligned} \left. \left( n v_\text{ax}-D_{ax}\frac{\partial n}{\partial z} \right) \right|_{z=0} = v_\text{ax} n_{in,x}, \qquad \left.\frac{\partial n}{\partial z}\right|_{z=L}=0. \end{aligned}\]

The mass balance equation for the solute \(c(t, z)\colon [0,T-\text{end}] \times [0,L] \mapsto \mathbb{R}^+\) is given by

\[\begin{aligned} \frac{\partial c}{\partial t} = -v_\text{ax} \frac{\partial c}{\partial z} +D_{ax} \frac{\partial^2 c}{\partial z^2} -\rho k_v \left( B_0x^3_c + 3\int_{x_c}^{\infty} v_{G}n x^2 \;\mathrm{d}x \right). \end{aligned}\]

As for the particle phase, the solute mass concentration subjects to the Danckwerts boundary conditions

\[\begin{aligned} \left.\left( c v_\text{ax}-D_{ax}\frac{\partial c}{\partial z} \right) \right|_{z=0} = v_\text{ax} c_{in}, \qquad \left.\frac{\partial c}{\partial z}\right|_{z=L}=0. \end{aligned}\]

Constitutive equations

Constitutive equations describe the kinetic processes in the governing equations. The relative supersaturation \(s>0\) is:

\[\begin{aligned} s=\frac{c-c_{eq}}{c_{eq}}, \end{aligned}\]

where \(c_{eq}>0\) is the solute solubility in the solvent. The nucleation kinetics can be split into primary and secondary nucleation:

\[\begin{aligned} B_0 = B_p + B_s, \end{aligned}\]

Which are in turn defined by the following constitutive equations. An empirical equation for primary nucleation is given by:

\[\begin{aligned} B_p=k_ps^u, \end{aligned}\]

where \(k_p\in\mathbb{R}^+\) is the primary nucleation rate constant and \(u\in\mathbb{R}^+\) is a constant. An empirical power-law expression is used for the secondary nucleation:

\[\begin{aligned} B_s=k_bs^bM^k, \end{aligned}\]

where \(k_b\in\mathbb{R}^+\) is the secondary nucleation rate constant, \(b\in\mathbb{R}^+\) and \(k\in\mathbb{R}^+\) are system-related parameters and \(M\in\mathbb{R}^+\) is the suspension density defined as

\[\begin{aligned} M=k_v\rho\int_{0}^{\infty}n\ x^3\;\mathrm{d}x. \end{aligned}\]

The following expression for the growth rate is implemented:

\[\begin{aligned} v_{G}=k_gs^g(a+\gamma x^p), \end{aligned}\]

where \(k_g\in\mathbb{R}^+\) is the growth rate constant, \(\gamma\in\mathbb{R}^+\) quantifies the size dependence, and \(g, a, p\in\mathbb{R}^+\) are system-related constants.

For information on model parameters and how to specify the model interface, see Population balance model.