You're reading the documentation for a development version. For the latest released version, please have a look at v5.0.1.

CADET Introduction

Performing a forward simulation comprises several steps:

  • Setting up the model including all parameters

  • Defining connectivity and dynamic events

  • Setting up the simulator and actually running the simulation

  • Evaluating results (e.g., plotting)

In this tutorial, we will build a simple forward simulation with a breakthrough of one component using the following system:

../../_images/breakthrough_system.svg

For this purpose, we use CADET-Process, an object oriented Python frontend for CADET. CADET still must be downloaded (or built from source) as explained in the installation guide.

../../_images/cadet_architecture_overview.png

Fig. 1 Relations between CADET-Core, CADET-Python, and CADET-Process.

For more information on how to set up models using CADET-Python, a plain file based API for CADET, please refer to the CADET-Python Introduction.

1. Setting Up the Model

We first create a ComponentSystem. The ComponentSystem ensures that all parts of the process have the same number of components. Moreover, components can be named which automatically adds legends to the plot methods.

from CADETProcess.processModel import ComponentSystem

component_system = ComponentSystem()
component_system.add_component('A')

Inlet Model

In CADET, the Inlet pseudo unit operation serves as a source for the system and is used to create arbitary concentration profiles as boundary conditions. The concentration profile is described using a piecewise cubic polynomial (cubic spline in the continuous case) for each component, where the pieces are given by the time sections. In this example we set a constant inlet concentration of 1 mM.

from CADETProcess.processModel import Inlet

inlet = Inlet(component_system, name='inlet')
inlet.flow_rate = 6.683738370512285e-8  # m^3 / s
inlet.c = [[1.0, 0, 0, 0]]  # mol / m^3

Column Model

Adsorption Model

Every unit operation model can be equipped with an adsorption model. The available models are listed in the binding model chapter.

For the Langmuir model, we use the Langmuir class. Then, we decide if we want to use the rapid-equilibrium assumption in the binding model (binding_model.is_kinetic = False), which is not the case here (dynamic binding). Finally, the parameters of the binding model have to be set for each component (they are vectors of length n_components). All model parameters can be listed using the parameters attribute. In case of the Langmuir model, we have to specify the parameters adsorption_rate, desorption_rate, and capacity.

from CADETProcess.processModel import Langmuir

binding_model = Langmuir(component_system, name='binding_model')
binding_model.is_kinetic = True
binding_model.adsorption_rate = [1.0, ]  # m^3 / (mol * s)   (mobile phase
binding_model.desorption_rate = [1.0, ]  # 1 / s (desorption)
binding_model.capacity = [100.0, ]  # mol / m^3   (solid phase)

General Rate Model

We now add a second unit operation, the column model. For the general rate model model, we use the GeneralRateModel class. In this class, we set the parameters related to transport and column geometry.

from CADETProcess.processModel import GeneralRateModel

column = GeneralRateModel(component_system, name='column')
column.binding_model = binding_model

column.length = 0.014  # m
column.diameter = 0.02  # m
column.bed_porosity = 0.37  # -
column.particle_porosity = 0.75  # -
column.particle_radius = 4.5e-5  # m

column.axial_dispersion = 5.75e-8  # m^2 / s (interstitial volume)
column.film_diffusion = [6.9e-6]  # m / s
column.pore_diffusion = [7e-10, ]  # m^2 / s (mobile phase)
column.surface_diffusion = [0.0]  # m^2 / s (solid phase)

Note that film, pore, and surface diffusion are all component-specific, that is, they are vectors of length n_components.

Initial Conditions

Next, we specify the initial conditions (concentration of the components in the mobile and stationary phases) for the column. These concentrations are entered as vectors, where each entry gives the concentration for the corresponding component. In this example, we start with an empty column.

column.c = [0]
column.cp = [0]
column.q = [0]

The OUTLET is another pseudo unit operation that serves as sink for the system.

Note

In this case, the outlet unit is actually not required. We could use the outlet concentration signal of the column model instead.

from CADETProcess.processModel import Outlet

outlet = Outlet(component_system, name='outlet')

System Connectivity

The connectivity of unit operations is defined in the FlowSheet class. This class provides a directed graph structure that allows for the simple definition of configurations for multiple columns or reactor-separator networks, even when they are cyclic. We add the previously defined units to the flow sheet and add connections between them.

from CADETProcess.processModel import FlowSheet

flow_sheet = FlowSheet(component_system)

flow_sheet.add_unit(inlet)
flow_sheet.add_unit(column)
flow_sheet.add_unit(outlet, product_outlet=True)

flow_sheet.add_connection(inlet, column)
flow_sheet.add_connection(column, outlet)

Note

Since the flow in the column models is incompressible, the total entering flow rate must equal the total outgoing flow rate. This restriction does not apply to a CSTR model, because it has a variable volume.

Process properties

The Process class is used to define dynamic changes of model parameters or flow sheet connections. This includes the duration of a simulation (cycle_time). To instantiate a Process, a FlowSheet needs to be passed as argument, as well as a string to name that process.

from CADETProcess.processModel import Process

process = Process(flow_sheet, 'Langmuir Breakthrough')
process.cycle_time = 1000.0

3. Setting Up the Simulator and Running the Simulation

To simulate a Process, a simulator needs to be configured. The simulator translates the Process configuration into the API of the corresponding simulator.

from CADETProcess.simulator import Cadet

process_simulator = Cadet()

simulation_results = process_simulator.simulate(process)

4. Plotting the Results

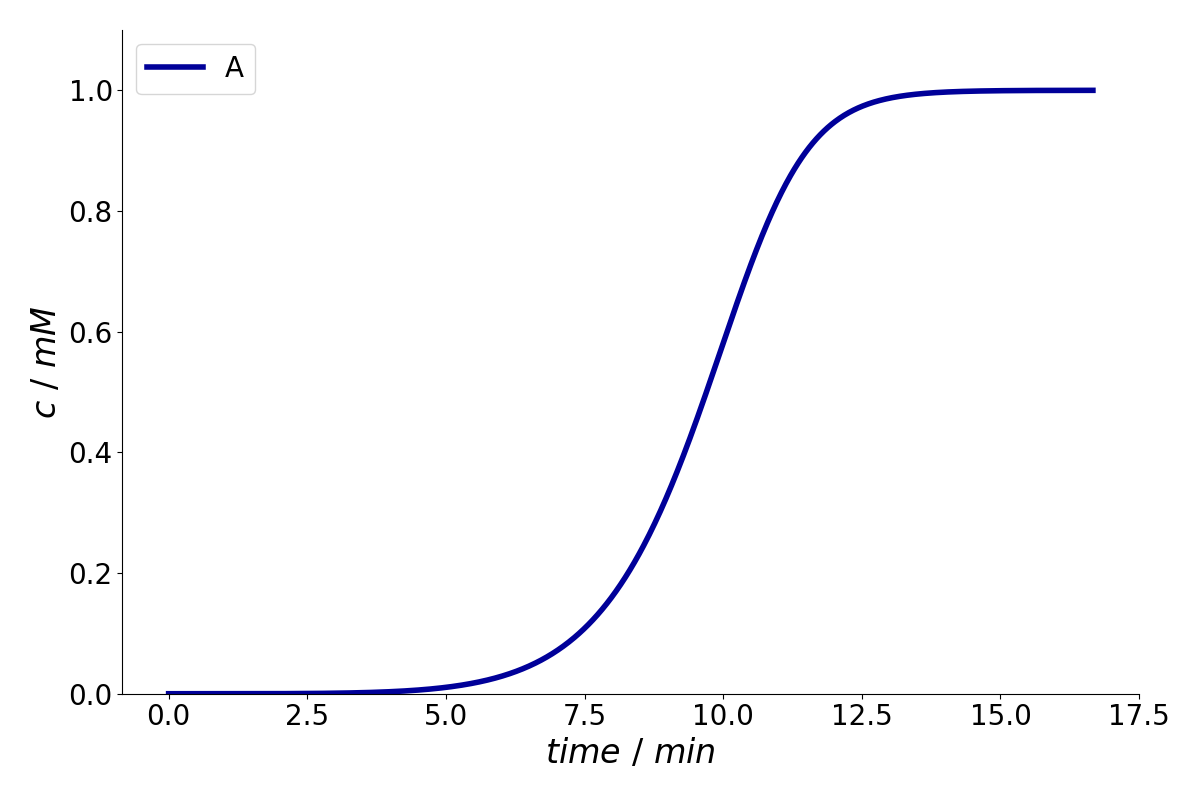
The data is stored in the .solution group of the SimulationResults object. Finally, we plot the concentration signal at the outlet of the column.

simulation_results.solution.column.outlet.plot()
../../_images/breakthrough_chromatogram1.png

For further details on the front-end and more examples please refer to the CADET-Process documentation.